When making a flight plan, there are numerous factors that come into play, from the weather to the route, including fuel, airport protocols, and much more. And among all these elements there are a series of calculations that the crew must carry out so that the flight operates under the maximum safety guarantees. In this article we are going to see those mathematical calculations in planning a flight.
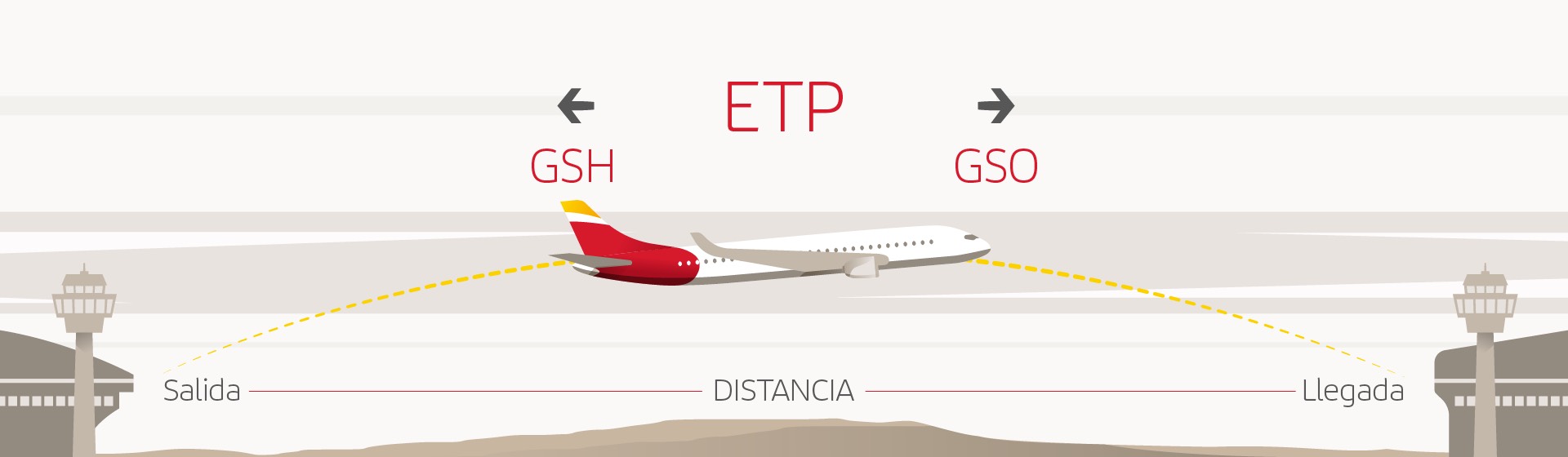
Equal Time Point (ETP)
In the strict sense, this is that point at which an aircraft takes the same time to reach its destination as it does to return to the point of origin. An ETP can also be established on a specific leg of the flight and not on the entire journey. But the important thing is that while you would expect it would fall at a route’s exact midpoint, this turns out to not usually be the case, largely thanks to the wind factor. It would be if the wind were calm, but this rarely happens. We must take into account, to make the calculation, the wind factor, including headwinds and tail winds which can speed an aircraft´s progress up or slow it down.
We therefore are left with the following factors:
DIST – the distance between the starting point and the arrival point (whether the entire route or a section of it) and which is recorded as DIST;
GSH – the speed of the plane returning to the airport of origin
GSO – the speed of the aircraft towards the destination airport
And so the formula would look like this:
ETP = DIST x GSH / GSH + GSO
By recording both the outward speed and the return speed on the route to be covered, we´ve included the wind factor, which will play in the aircraft´s favour in one direction and against it in the other. So it would look a bit like this:
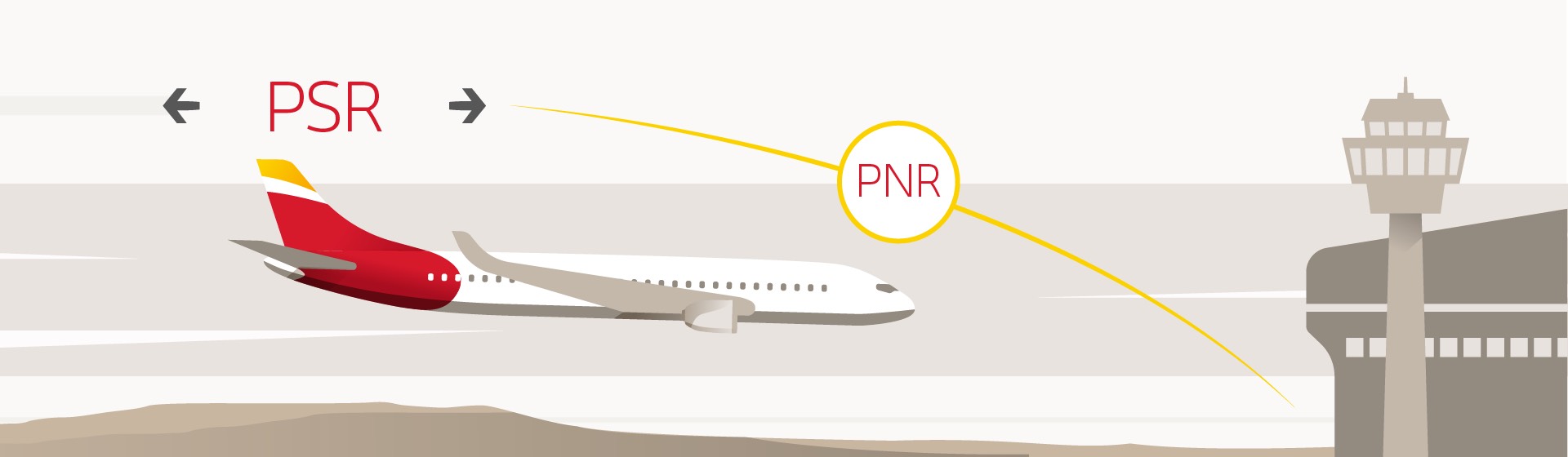
Point of Safe Return (PSR)
The PSR is that point on the route from which the aircraft could return to the airport of origin with fuel reserves intact. In this mathematical operation the elements that come into play are.
END – Aircraft range (expressed in hours) less fuel reserves and recorded as
GSH – again, the speed of the aircraft returning to the point of origin
GSO – again, the aircraft´s speed towards the destination point
So the formula to calculate the safe return point will be:
PSR = END – FR x GSH / GSH + GSO

Point of No Return (PNR)
Taking into account the threshold obtained in the previous calculation, we’ll also be able to determine the PNR, the point on the route from which a airplane would be unable to return to its point of origin and would have to opt for another destination. This point of no return determines the maximum distance that it can travel from where it takes off.
As we have seen in the two previous formulas, the calculation isn’t not linear, not as simple as calculating when exactly half of the fuel remains, since the factors going speed and return speed come into play. The weather and the wind in favor or against determine these speeds.
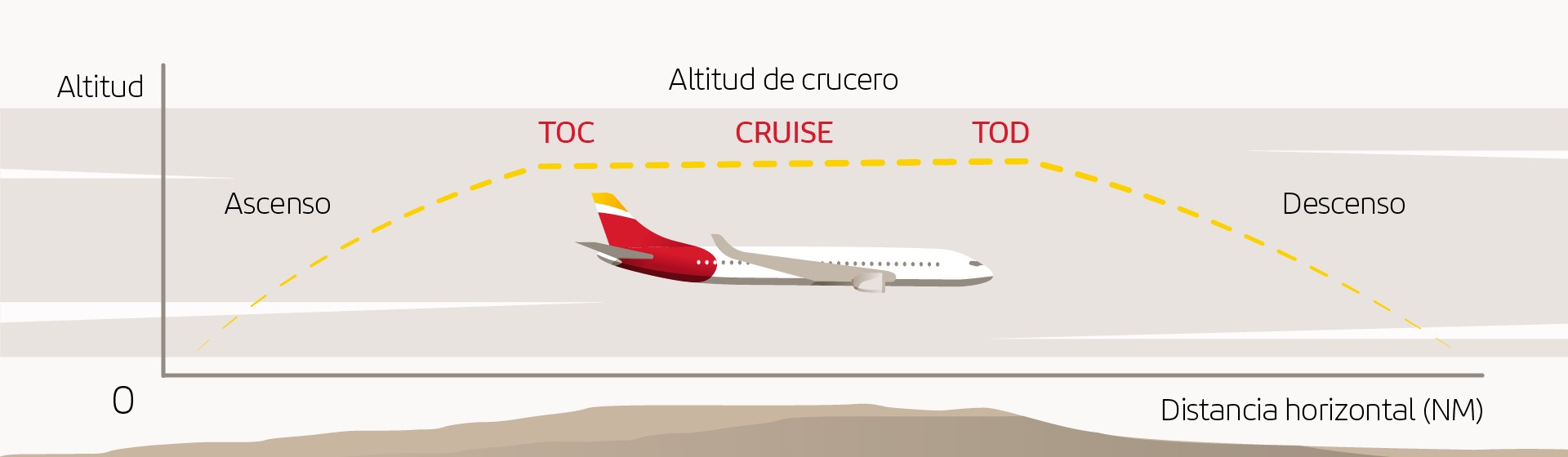
Top of Climb (TOC)
This is the point at which the aircraft reaches its so-called cruising altitude after takeoff. These are the factor which come into play
- altitude above sea level of the airport of origin
- the aircraft´s target altitude
- rate of climb
- horizontal speed
- weather conditions
First we need to divide how much the plane climbs by the rate of climb expressed in minutes. The total metres (or feet) of elevation will result from subtracting the altitude above sea level of the takeoff airport. This is how we will obtain the speed:
Time = (final altitude-initial altitude)/climb rate (feet per minute)
On the other hand, time due to speed will give us OCD. Therefore:
TOC (in nautical miles) = Time x Speed (in knots)
In this formula the wind is not taken into account; but the pilot will then add or subtract said wind from the speed in the operation, depending on whether it plays in favour or against the direction of flight.