
One of the first things we learn in school about geometry (more specifically, plane geometry) is that the shortest distance between two points is a straight line. Obvious, isn’t it? And yet…
The fact is, this obvious truism is only true in two dimensions, as on a flat map, which is how we usually think of the world. But when it comes to spherical geometry – and, unless you’re a Flat Earther, our planet is more or less a sphere – that’s simply not the case.
If you’ve ever tried to flatten out an apple peel or orange rind on a table, you’ve surely noticed how it tends to crack at certain points. Something similar happens – and thus certain allowances must be made – when we try to render a sphere on paper (even though the Earth isn’t a perfect sphere).
For example, in the very common Mercator projection (used, among many others, by Google Maps), Greenland appears to be as large as the entire continent of Africa, when in reality the latter is something like 14 times bigger than the former; similary, Alaska and Brazil appears to be similar in size, when in reality Brazil is five times larger.
These two factors combined – and finally we’re getting more to how this all relates to aviation – can sometimes lead us to automatically think of all routes between origin and destination airports as straight lines, but oftentimes this can be considerably off base, depending on the airport pairs, the distance between them, and their differences in latitude.
When it comes, for example, to the Madrid-New York route, the shortest distance on the following map is not the black line but the red one:
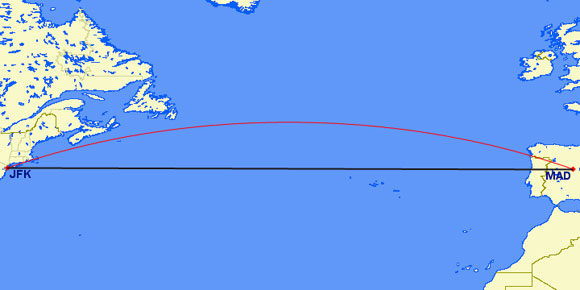
The reason for this is that on a spherical surface the shortest line between two points is the arc of the “great circle” which joins them, and this is represented on a flat map by the red line.
Madrid and New York are more or less at the same latitude, but if we were to choose the route between New York and Tokyo, even just five degrees difference in latitude ends up multiplying the routing differences considerably, leading to a rather counter-intuitive route:
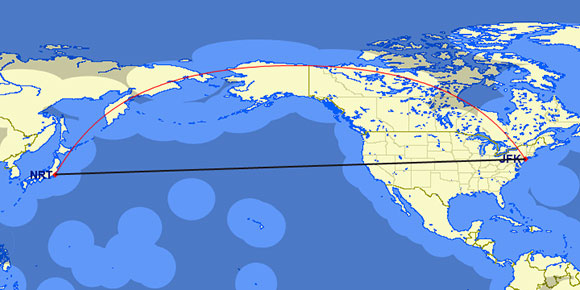
Surprisingly, this flight takes place almost entirely over land and less than 60 minutes’ flight from an airport (as shown by the lighter areas on the above map), so that an airplane flying this route would not need ETOPS certification.
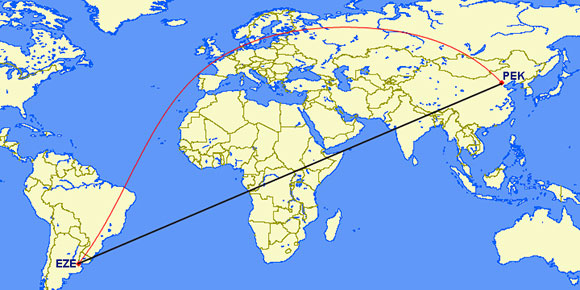
A third, even more pronounced example would be a flight between Beijing and Buenos Aires – assuming there were an aircraft capable of flying nonstop a route with 75 degrees of separation in latitudes.
Given all the above, it would be natural to assume that any aircraft would unfailingly follow the routes delineated by the great circle between two airports. But in actuality there are some cases in which it wouldn’t. For example, there are zones that are off limits to civilian air traffic. Also, weather or other conditions such as an erupting volcano might come into play.
Another reason for rerouting in various parts of the world but especially in the case of transatlantic crossings or flights across North America, would be jet stream conditions which would make it preferable to deviate from the great circle route rather than fight against jet stream headwinds.
Also, not all airlines have aircraft equipped and certified for polar crossings, such as required by the aforementioned New York-Beijing route. ETOPS certification specifies the maximum distance a given aircraft may fly from a given airport. And to complicate matters even further, for safety reasons on trans-Atlantic flights, the established set of routes changes daily according to jet stream conditions.
Lastly, within Europe as well as in other areas of the world where air traffic is particularly dense, there are air lanes to which flights must adhere to but which often do not coincide with great-circle routes.
There are also undoubtedly other restrictions out there, but you get the idea. In any case, no worries, because if you take a look at Iberia’s in-flight magazine Ronda, you’ll see that its route also relies on straight lines, just the same as all other airlines I’ve ever seen.
All the maps included in this post were created with Karl L. Swartz’ Great Circle Mapper, a tool which, incidentally, is great fun for us aviation geeks.

